无约束优化算法总结
机器学习的优化目标一般可以表示成Obj = Loss + regularization,有了这样一个优化目标剩下就是如何求解最小化问题了。机器学习绝大多数Obj都是非线性的,很难有形式解,这时需要各种近似优化算法来求Obj的极小化。如果Obj是凸函数,那么极小值等价于全局最小值,否则极小值未必是全局最优值。这里将Obj抽象为f(x),并假设f为凸函数,且二阶连续可导。
梯度下降法
这个很常见也很简单,参数修正方向就是负梯度方向,步长可以定长也可以单独优化,即Xk+1 = Xk – lambda*grad.
牛顿法
牛顿法最初就是用来迭代求解方程根,想必大家高中时候都接触过。原理是利用泰勒公式在x0处一阶展开,即f(x)=f(x0)+f’(x0)(x-x0)。求解方程f(x)=0得,x=x1=x0-f(x0)/f’(x0),由于泰勒展开只是近似等价,所以这里的x1也只是比x0更接近f(x)=0的近似解,所以需要不断的迭代来逼近真实x。牛顿法通过下图一目了然:
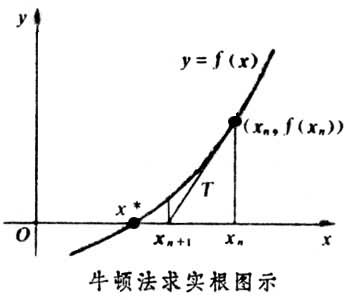
牛顿法不是用来求根的吗,那怎么用来求最优化?直观的,求f(x)的最小值,必要条件是f’(x)=0,so,可以用牛顿法来求f’(x)=0的解!
下面还是来公式推导下,还是利用泰勒公式,二阶展开,f(x+deltax)=f(x)+f’(x)deltax+1/2f’’(x)deltax^2。当deltax无限趋近于0,上面式子近似为f’(x)deltax+f’’(x)deltax^2=0,即deltax = - f’(x)/f’’(x)。所以迭代公式为xk+1 = xk-f’(x)/f’’(x)。
牛顿法比梯度下降更容易收敛,速度更快,一般认为牛顿法利用了曲线更多的信息(二阶导数)。根据wiki上的解释,从几何上说,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径(from 知乎)。如下形象图,红色曲线是利用牛顿法迭代求解,绿色曲线是利用梯度下降法求解。
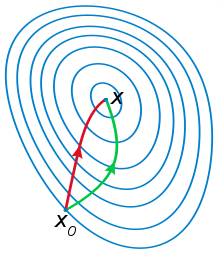
扩展下对于多元x,梯度变为梯度向量,二阶导变为海森矩阵(Hessian matrix),分别用字母g和H表示,迭代方向变为-H^-1g称为牛顿方向。


阻尼牛顿法相比牛顿法增加了步长lambda的精确搜索。
拟牛顿法
牛顿法存在两个主要缺点:
1. 需要计算海森矩阵和它的逆,计算复杂度高而且空间复杂度为O(N^2)
2. 有时海森矩阵无法保证正定,算法失效。
针对上面问题,研究者提出拟牛顿法(Quasi-Newton methond),基本思想是不直接求海森阵或其逆,而是通过梯度构造出海森矩阵(或其逆)的近似,而且是正定对称的。
符号上用B表示对海森矩阵H的近似,D表示对逆矩阵H^-1的近似,Sk=Xk+1-Xk,yk=gk+1-gk。
各种拟牛顿法都需要满足拟牛顿条件:yk=Bk+1Sk或者Sk=Dk+1yk。下面大致介绍下DFP/BFGS/L-BFGS拟牛顿算法。
1. DFP算法

在步骤3还需要计算gk+1,下同。
2. BFGS算法

这时从海森阵计算逆计算量也不小,通过Sherman-Morrison公式,可以直接得到B的逆的递推关系,将B的逆替换为D,这样我们得到另一种BFGS。
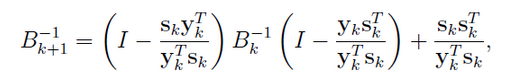

3.L-BFGS算法
上面的拟牛顿法都没有解决空间复杂度O(N^2)的问题,为了解决该问题,我们就不能存储海森或其逆矩阵了。想想时间换空间,我们就只能存储生成海森的s和y向量了,需要海森时计算得出。而且,向量s和y也不是所有都存,而是固定存最新的m组。每次计算D时,只利用最新的m组s和y,这样空间复杂度降到了O(mN).
若记ρk=1/yk^T*sk,Vk=I-ρkyksk^T,算法2.3的步骤6可以近似为
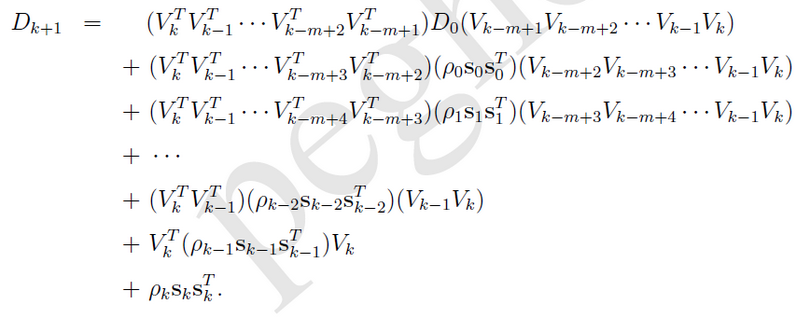
由于V和ρ标号增加方向相反所以需要前后分别遍历,总计两次遍历才能计算D。
由BFGS算法流程可知,求Dk*gk获取搜索方向才是最终目的,因此论文(updating quasi-newton matrices with limited storage)设计出了一种Dk*gk快速算法:

注意倒数第二行beta应该是i下标,最后算出的rL即为Dk*gk的值。
后记
本文算法截图来自博客(http://blog.csdn.net/itplus/article/details/21897715) ,感谢原作者的分享。
上面讨论的都是f(x)可导的情况,针对不可导还有一些变种算法,比如OWL-QN,有时间再研究总结。

